The Tower of Hanoi

The Tower of Hanoi is a math­e­mat­i­cal puz­zle, of­ten in­tro­duced to un­der­grad­u­ate col­lege stu­dents. At face value, the puz­zle seems point­less. You are sim­ply mov­ing discs around. Yet, some­thing is in­ter­est­ing about the puz­zle’s na­ture. After care­ful in­spec­tion, it turns out we can con­jure up a con­cise re­cur­sive al­go­rithm. If your not fa­mil­iar with re­cur­sion, con­sider check­ing out my pre­vi­ous post. In a nut­shell, re­cur­sion is use­ful when a prob­lem can be bro­ken down into smaller prob­lems of the same form as the orig­i­nal. With some imag­i­na­tion, the Tower of Hanoi meets this re­quire­ment.

Why?

And you may be won­der­ing why you should care. After all, there is an it­er­a­tive so­lu­tion to the puz­zle—just do a Google search. Well, this toy prob­lem shows that re­cur­sion can in­spire sim­pler code than it­er­a­tion. Although I’m not go­ing to cover the it­er­a­tive so­lu­tion ex­plic­itly here, you should look it up. By com­par­ing the two so­lu­tions, it’s clear that the re­cur­sive one fea­tures less code and eas­ier to read.

Given the para­graph above, I am go­ing to em­pha­size that re­cur­sion is­n’t a su­per­flu­ous, com­pli­cated tech­nique. It has le­git­i­mate uses in the real world. If it will make your code eas­ier to write and un­der­stand, con­sider us­ing it. Now, it’s not al­ways bet­ter. You should also be aware of the per­for­mance trade­offs—par­tic­u­larly in lan­guages with­out tail call op­ti­miza­tion.

The Rules

For those un­fa­mil­iar with the puz­zle, I’ll quickly ex­plain the rules. There is a board with three poles and an arrange­ment of disks. The disks are each of a dif­fer­ent size, and ini­tially, they are arranged in a cone shape on a sin­gle pole. The goal is to move all the disks–one at a time–to an­other a pole, once again form­ing the cone shape. Also, a larger disk can­not be stacked on top of a smaller disk at any time.

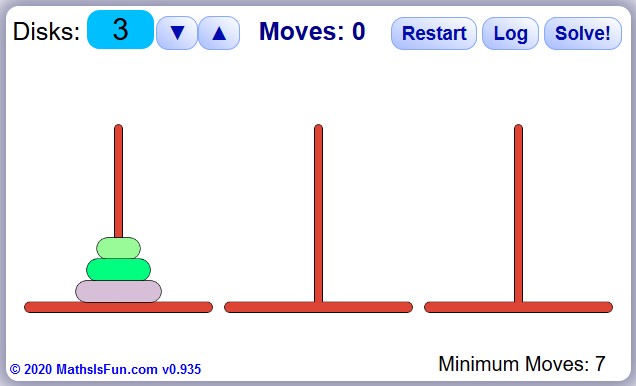
Recursive Solution

Once again, the Tower of Hanoi can be solved re­cur­sively. It works be­cause we can split the game into sub­puz­zles. These sub­puz­zles are them­selves a miniver­sion of The Tower of Hanoi–which can then be solved in the same fash­ion as the big­ger ver­sion. To note, the al­go­rithm will al­ways pro­duce a valid set of game-win­ning moves. So you can win the game every time.

Before jump­ing into the code, let’s imag­ine what the so­lu­tion’s struc­ture could look like. To start, we’ll la­bel the three poles A, B, and C. Then, let’s say there’s a stack of h disks on pole A. This arrange­ment is the ini­tial setup–no sur­prises here. As a re­minder, to win, the player needs to move all the disks to an­other pole.

Yet, to move pole A’s largest disk, h-1 disks need to be shuf­fled to an aux­il­iary pole–let’s say pole B. Of course, this is just solv­ing a slightly smaller ver­sion of the same puz­zle. So, we need to move h-2 disks some­where… You should see where this is go­ing.

What hap­pens when we have re­duced our way to sub­puz­zle con­sist­ing of one disk? This sit­u­a­tion is the eas­i­est to han­dle–just move di­rectly move the disk to the tar­get pole–in this case pole C.

Now, in gen­eral, once the largest disk of a sub­puz­zle has moved been moved the tar­get pole, we can then move all the disks placed on the aux­il­iary pole over to the tar­get pole as well. To do this, we are again just solv­ing a smaller ver­sion of the puz­zle–we are just chang­ing which poles are la­beled as the aux­il­iary and the tar­get.

In sum­mary, we are re­peat­edly mov­ing the large disk of a sub­puz­zle af­ter the smaller disks above have been moved to the aux­il­iary pole. The key is to cor­rectly track which poles should be the tar­get and the aux­il­iary as the al­go­rithm twists through the self calls. Assuming we do this cor­rectly, the puz­zle will be solved by solv­ing all the sub­puz­zles in turn.

Some Code

Let’s stop talk­ing the­ory and look at some code. Below, I wrote a so­lu­tion in Racket that al­lows you to change the num­ber of disks. Since im­mutable data struc­tures are used, the code is a lit­tle dif­fer­ent than what you typ­i­cally find on the Internet; how­ever, the core con­cepts are still the same. You should be able to map my nat­ural lan­guage de­scrip­tion to the code. At the very least, note what the base case is and how the prob­lem space is re­duced every self call.

#lang racket

(struct board (A B C) #:transparent)

(define (new-board size)
  (board (range 1 (add1 size)) '() '()))

(define (pop stack)
  (cond
    [(empty? stack) '()]
    [else (cdr stack)]))

(define (peak stack)
  (cond
    [(empty? stack) '()]
    [else (list (car stack))]))

(define (move brd pole1 pole2)
  (define table
    (hash 'A (board-A brd)
          'B (board-B brd)
          'C (board-C brd)))
  (define (check stack pole)
    (cond
      [(eq? pole pole1) (pop stack)]
      [(eq? pole pole2) (append (peak (hash-ref table pole1)) stack)]
      [else stack]))
  (board (check (board-A brd) 'A) (check (board-B brd) 'B) (check (board-C brd) 'C)))

(define (solve size)
  (cond
    [(<= size 2) (raise-user-error "Size must be greater than two")]
    [else
     (define board (new-board size))
     (helper size board 'A 'C 'B)]))

(define (helper n brd source target auxiliary)
  (cond
    [(n . > . 0)
     (define new-brd-1 (helper (sub1 n) brd source auxiliary target))
     (define new-brd-2 (move new-brd-1 source target))
     (displayln new-brd-2)
     (helper (sub1 n) new-brd-2 auxiliary target source)]
    [else brd]))
    
(module+ main
  (solve 3))

Here’s the out­put from the code–with the size pa­ra­me­ter set to three. The left-hand side is the top of each stack. With a lit­tle squint­ing, you should be able to trace out the cor­rect se­ries of moves to solve the puz­zle.